在金融市场的叙事中,我们总是被英雄主义所吸引。每隔几年,媒体就会推崇一位业绩惊人的“民间股神”或“天才基金经理”。他们不仅在牛市中斩获颇丰,甚至在熊市中也能全身而退。对于普通投资者而言,这种持续的成功似乎是某种深不可测的“洞察力”或“盘感”的体现。
然而,如果我们剥离掉这些充满传奇色彩的外壳,从纯粹的概率论与统计学视角审视,会发现一个令人不安的真相:在样本基数足够大的情况下,仅仅依靠随机性(Randomness),市场也足以筛选出看起来像“天才”的幸存者。这种逻辑上的陷阱,被称为幸存者偏差(Survivorship Bias)。
为了量化理解幸存者偏差,我们可以设定一个极其简化的思想实验。
假设有 1,024 名对金融知识一窍不通的人参加一场“预测比赛”。规则非常简单:每人每天预测第二天股市的涨跌(只有“涨”和“跌”两个选项)。
第一天:根据概率,大约有 512 人猜对,512 人猜错。猜错者离场。
第二天:剩下的 512 人继续预测。大约有 256 人连续两天猜对。
第三天:剩下的 256 人中,大约有 128 人连续三天猜对。
以此类推,到了第十天,统计学告诉我们,样本中依然会剩下1 个人。
对于这位“十连胜”的幸存者来说,他已经连续 1,024 次中脱颖而出。此时,大众会如何看待他?媒体可能会称他为“精准预判市场拐点的预言家”,而他本人在巨大的成功面前,也极易产生心理学上的“自利归因”倾向,将这段纯粹的运气总结为一套深奥的“交易哲学”。
但作为上帝视角的观察者,我们深知:这个结果完全源于随机波动。 无论这 1,024 个人的预测逻辑是看星盘、看天气还是扔硬币,最终都会产生一个“十连胜”的幸存者。这个幸存者的出现,是概率分布的必然结果,而非个体能力的体现。
在现实的投资世界中,情况远比扔硬币复杂,因为真实的能力(Skill)确实存在。问题的核心在于:我们如何通过科学的方法,将不可复制的“运气成分”从总收益中剥离出来?
量化投资领域通常引入“统计显著性检验(Statistical Significance Testing)”来解决这一难题。
1. 均值回归与 p 值(P-value)
在统计学中,我们首先设定一个“虚无假设”(Null Hypothesis):假设某位投资者的超额收益完全是由随机运气产生的。
随后,我们计算该投资者的实际收益率分布。如果该收益率出现的概率(即 p 值)极低(通常小于 0.05 或 0.01),我们才有理由推翻虚无假设,承认其表现具有“统计显著性”。
简而言之,如果一个人连赢 10 把硬币的概率是 1/1024(约为 0.0009),这在统计学上是显著的。但前提是,我们必须知道有多少人参与了最初的比赛。如果全世界有 100 万人同时在扔硬币,那么出现几个“十连胜”的人不仅不是奇迹,反而是数学上的必然。
2. t 统计量与夏普比率
对于职业投资者,我们不仅看收益的高低,更看收益的稳定性。
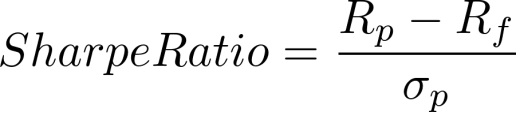
其中,Rp为投资组合收益率,Rf为无风险利率,σp为收益率的标准差。
如果一个人的高收益伴随着极高的波动,那么这种收益往往带有强烈的随机色彩。相反,一个能够维持高夏普比率、且交易频率极高的策略,其“能力”成分的占比通常更高。
与个体投资者或单一策略基金不同,平台型基金的优势在于通过制度设计和多空策略组合,最大程度地对冲掉随机性风险。
1. 多样化子策略的“大数定律”
单一交易员可能因为运气连续获利,但如果平台同时运行数十个逻辑互补的子策略,情况就会发生变化。根据大数定律(Law of Large Numbers),随着独立博弈次数的增加,观察到的结果会越来越接近其理论期望值。
在平台视角下,如果我们将资源分配给多个具有微弱正向期望(Edge)的策略,个体管理人的随机性扰动就会在集合层面被相互抵消,最终沉淀出稳定的、具备数学必然性的收益曲线。
2. 严苛的样本外检验(Out-of-Sample)
为了规避幸存者偏差,平台型基金在引入新策略或管理人时,会进行严苛的穿透式归因:
回测过拟合检测: 排除那些通过“暴力搜索”历史数据寻找偶然规律的策略。
样本外验证: 策略必须在未参与开发的历史“盲区”或实时模拟盘中表现一致。
风险因子剥离: 利用风险模型(Risk Models)剥离掉市场风格(如小盘股风格、高杠杆风格)带来的 Beta 收益,只为纯粹的、可复制的 Alpha 付费。
结语
金融市场是一个巨大的、充满干扰的随机场。幸存者偏差像一面哈哈镜,将运气的偶然放大成了能力的必然。
作为平台型基金,我们深知“股神”易求,而“显著性”难得。科学投资的第一步,是承认随机性的存在,并保持对市场的敬畏。与其寻找那位“扔硬币的冠军”,不如构建一个基于数学规律、能够跨越周期、不依赖单一幸运儿的专业平台系统。
毕竟,运气会随时间流逝而均值回归,而数学规律,才是资本市场中的长情。